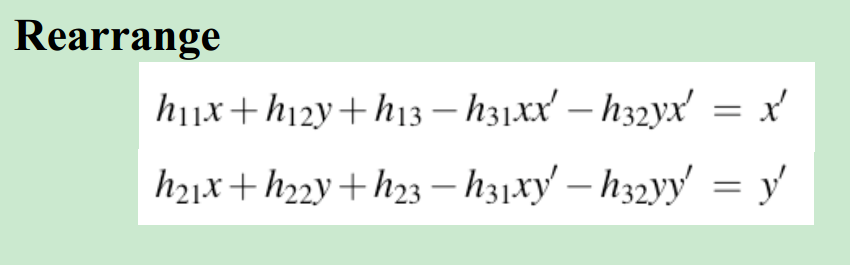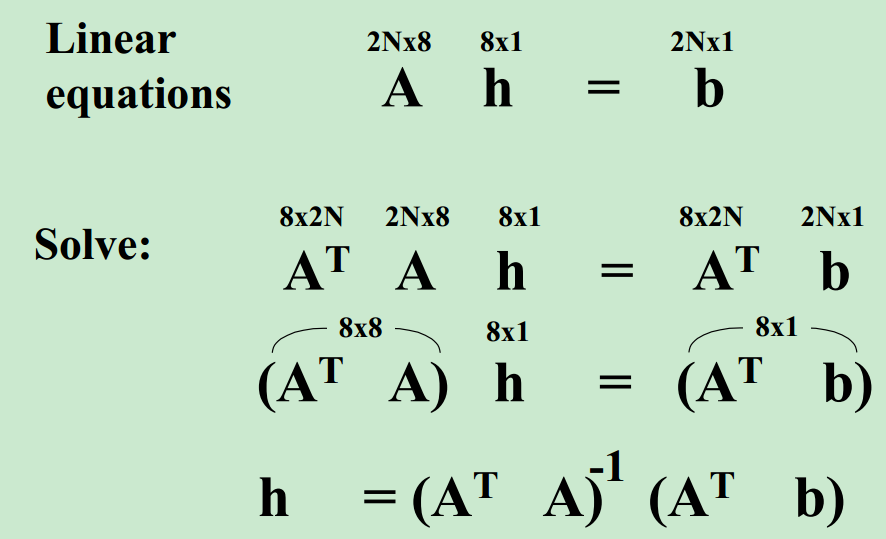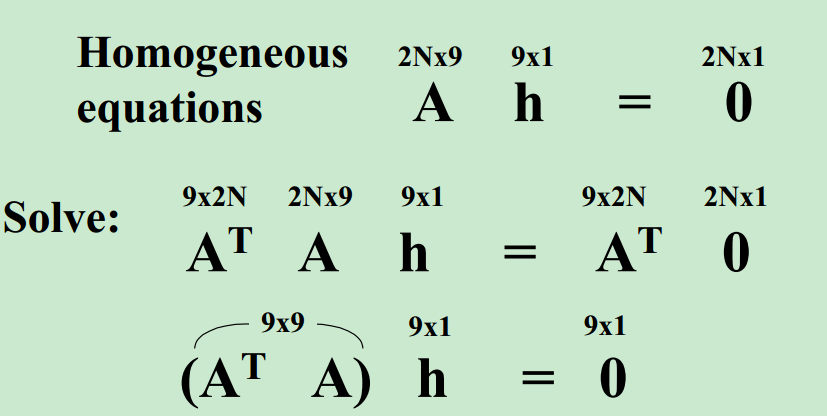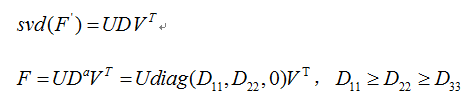本文共 6175 字,大约阅读时间需要 20 分钟。
本次打算梳理下最基本的几个矩阵之间的关系以及计算,总结大体内容:
1. 单应性矩阵的基本概念
什么是单应性矩阵?单应性变换包含什么样的射影组合(projective transformation)?
单应性关系的前提条件?
单应性与极几何的联系?
2. 单应性矩阵的计算
本质矩阵和基础矩阵的性质,上一篇博文有详细介绍,所以此处只讲计算方法了。
3. 基础矩阵的计算及计算前提条件
4.本质矩阵的计算
5.给定本质矩阵,如何提取相机朝向R和相对位移关系(基线方向T)
1. 单应性矩阵的基本概念
什么是单应性矩阵?
单应性是几何中的一个概念。单应性是一个从实射影平面到射影平面的可逆变换,直线在该变换下仍映射为直线。它是一对透视投影的组合射影变换群。它描述了当观察者视角改变时,被观察物体的感知位置会发生何种变化。射影变换并不保持大小和角度,但会保持重合关系和交比。
在计算机视觉领域中,空间中同一平面的任意两幅图像通过单应性关联在一起(假定是针孔相机)。比如,一个物体可以通过旋转相机镜头获取两张不同的照片(这两张照片的内容不一定要完全对应,部分对应即可),我们可以把单应性设为一个二维矩阵M,那么照片1乘以M就是照片2. 这有着很多实际应用,比如图像校正、图像对齐或两幅图像之间的相机运动计算(旋转和平移)等。一旦旋转和平移从所估计的单应性矩阵中提取出来,那么该信息将可被用来导航或是把3D物体模型插入到图像或视频中,使其可根据正确的透视来渲染,并且成为原始场景的一部分。
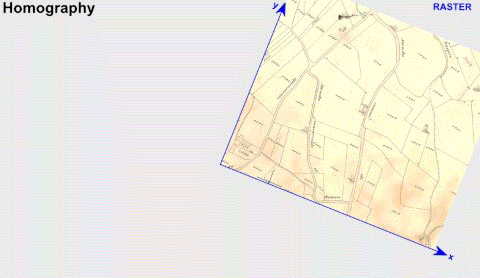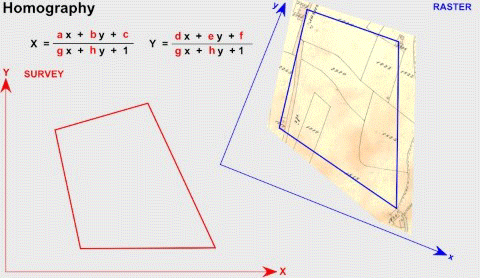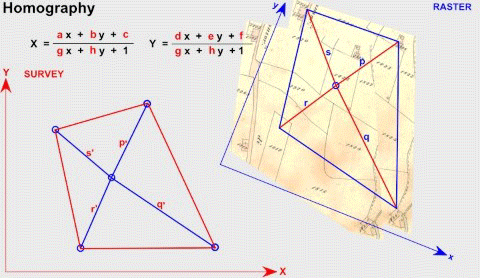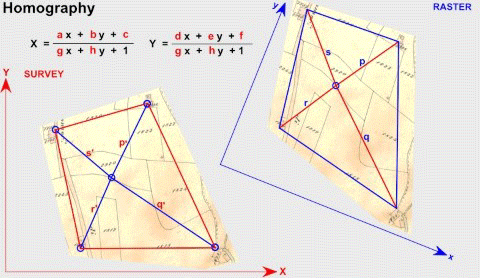
假设图A中有一个点x的坐标为(u,v,1),图B中对应匹配点x’坐标为(u’,v’,1),那么单应性矩阵可以将两个坐标联系起来:
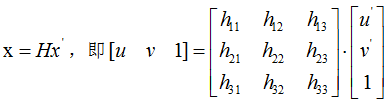
注意,这种单应性联系不依赖于观察场景结构,即无论相机拍摄什么画面,两个画面的单应性关系保持不变。
单应性变换包含什么样的射影组合(projective transformation)?
首先看等距变换Isometries transformation,它相当于是平移变换和旋转变换的复合。

上式也可以写作:
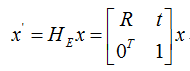
上式中ε等于正负1,当ε=1时,等距变换与原结构保持相同方向,即是欧氏变换,表达刚性物体运动;当ε=-1时,等距变换是逆向的。另外,R是正交矩阵。
等距变换有三个自由度,一个旋转,两个平移。等距变换后目标结构的长度、角度、面积与原结构相同。
再看相似变换(Similarity Transformation),它相当于是等距变换和均匀缩放的一个复合。
相似变换可以从两组匹配点计算出来,它有四个自由度,一个尺度,一个旋转,一个平移。相似变换后目标结构内部的角度、长度比、面积比保持不变。R是正交矩阵
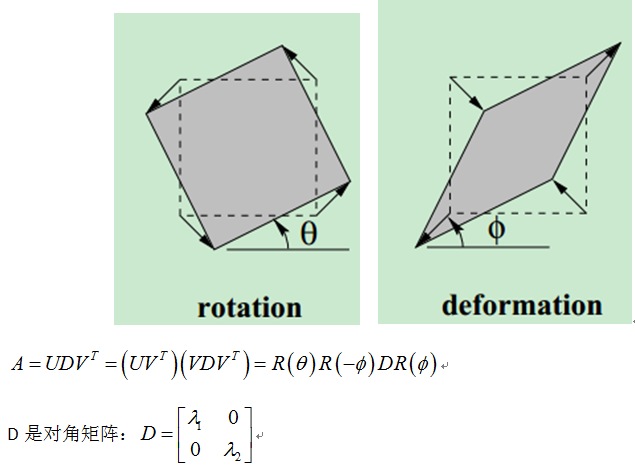
再看仿射变换(Affine Transformation),它相当于一个平移变换和一个非均匀变换的复合。

仿射矩阵A是2阶非奇异矩阵,A通过奇异值分解为旋转rotation和非均匀缩放deformation:
上式中U和V都是正交矩阵,对A简单描述下:λ1和λ2代表旋转后的目标在x和y方向的缩放比例,所以是非均匀的。Φ代表缩放的方向,θ代表旋转的方向。
仿射变换中A有六个自由度,2个尺度,2个旋转,2个平移。经过仿射变换后,原来平行的线还是平行的,并且平行线段的长度之比保持不变,面积之比也是不变的。另外仿射变换是否保向,取决于A的行列式值的正负。
最后看射影变换projectivetransformation,也就是单应性矩阵,他表达齐次坐标的非奇异线性变换。
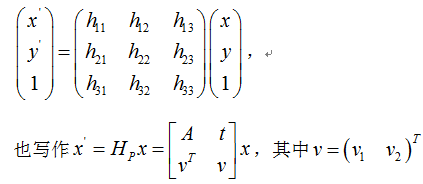
v是射影变换后平行直线可能不再平行的原因。
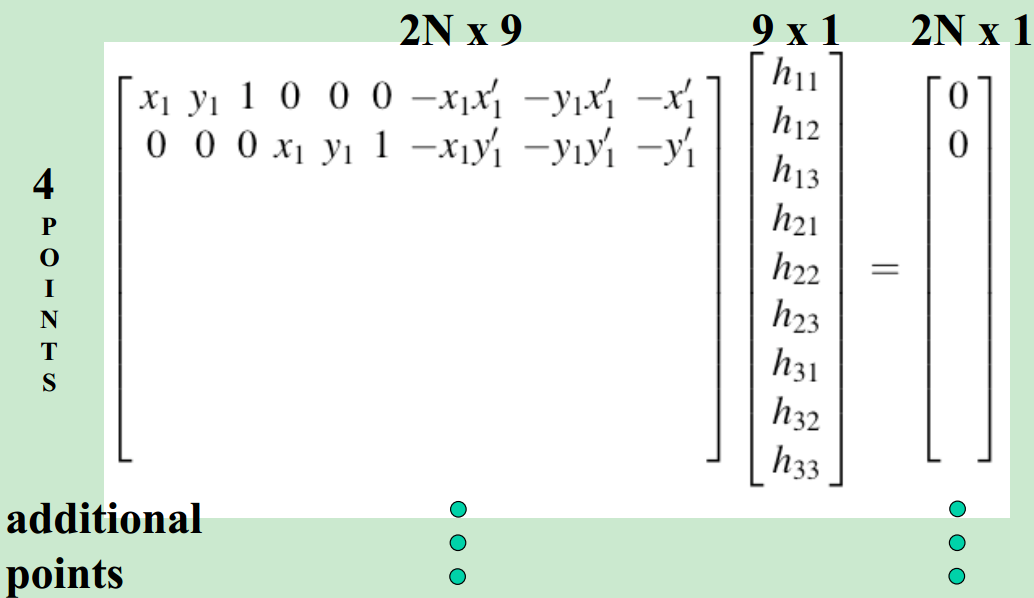
由于齐次坐标对于尺度具有不变性,可以从H中提取该尺度(比如v),因此单应性矩阵有8个自由度。两个平面之间的射影关系,可以通过4组匹配点计算得到(注意任意3点不可共线)。经过射影变换后,目标结构的交比cross ratio保持不变(两个平面上分别有4个点,平面1上线段AB与线段CD之比,等于平面2上线段A’B’与线段C’D’之比)。另外变换前后共点,共线,相切,拐点,切线的不连续性和岐点保持不变。
射影变换可以看作是一些列变换的组合:
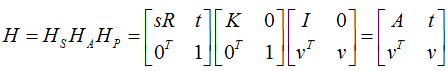
上三角矩阵K的行列式值为1,v不等于0,如果s的正负确定,则H是唯一的。
HP (2 dof) moves theline at infinity; HA (2 dof) affects the affine properties, but does not movethe line at infinity; and finally, HS is a general similarity transformation (4dof) which does not affect the affine or projective properties.
总结:
- 射影变换后,面积的缩放与位置有关,直线变换方向也与面积有关。
- 射影变换是不可逆的。
- 仿射变换位于射影变换和相似变换之间,仿射变换推广相似变换使得夹角不再保持不变,造成物体形状在变换后产生歪斜,他在变换中,直线只与方向有关,与位置无关,不会像射影变换那样,越远越小
下图中参数数量与上面不符,因为他针对的是3D点,上面是2D点

单应性关系的前提条件?
如果两幅图像之间的相机运动只有旋转而没有平移,那么这两幅图像通过单应性关联在一起(假定是针孔相机)。也就是说(if and only if):
a. Both images are viewing thesame plane from a different angle
b. Both images are taken from thesame camera but from a different angle.( Camera is rotated about its center ofprojection without any translation)
也就是说:
a.当两个相机所代表的视平面(image plane)相互平行,stereo normal case,单应性矩阵才是有效的。(baseline不为0,但是极点在无穷远)
b.当且仅当相机是绕相机中心旋转,没有偏移,baseline什么的都是零,单应性矩阵才是有效的。(baseline为0)
单应性与极几何的联系?
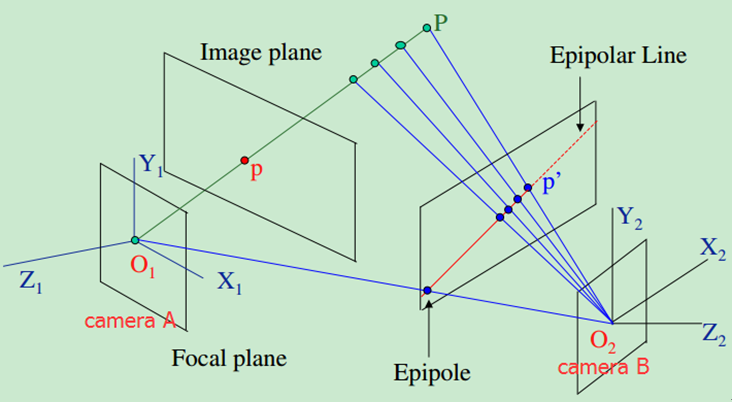
下图为极几何的经典视图,相机A的中心为O1,相机B的中心为O2,它们共同看到空间一点P。根据极几何的性质,空间中所有落在直线O1P上的点,最终都会落在在Image Plane B的极线上。
根据单应性的前提条件,单应性与极几何的区别在于两个相机主点之间的距离为0时,
总结起来:
当相机之间存在偏移,那么该用极几何关系描述点的对应关系,此时两个图片之间点的匹配依赖于物点的深度,即物点到相机的距离。
It maps a point in one image to a line in the other image. Actualmatching point depends on the depth of that point,that is its distance from thecamera
当相机之间不存在偏移时,极几何关系不再适用,该用单应性描述点的对应关系,此时两个图片之间点的匹配不依赖于物点的深度。(此时三角方程不成立)
It maps a point in one image to a point in the other image. Themapping does not depend on the depth (distance) of point to the camera. Thismakes sense because baseline z zero means ordinary stereo triangulationequations fail.
从下图看出相机拍摄时并未有偏移,故通过单应性做的图像拼接。

2. 单应性矩阵的算法
从单应性矩阵的定义出发:

除此之外,我们可以通过归一化坐标,使得h的结果是numerical stable。但是即使这样,这种做法对于噪声非常敏感,有几个outlier就完蛋了。
而第二种方法就很好,

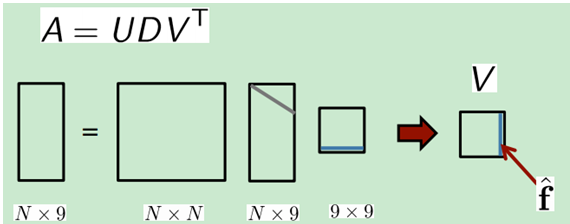
为了使上式为0,咱只要对左侧ATA进行奇异值分解,挑选奇异值前九个最小的v的列向量作为h即可,SVD:
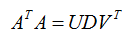
Let h be the column ofV (unit eigenvector) associated with the smallest eigenvalue in D.(if only 4points, that eigenvalue will be 0)
Matlab代码:
function H = find_H(P1, P2)% H = find_H(P1, P2)% % P1 are coordinates from source frame ([n*2], n>= 4)% P2 are coordinates from destination frame ([n*2], n>= 4)% H is the 3*3 homography matrix from P1 to P2% [P2; 1] ~ H [P1; 1]% x = P1(:, 1);y = P1(:, 2);X = P2(:, 1);Y = P2(:, 2);A = zeros(length(x(:))*2,9);for i = 1:length(x(:)), a = [x(i),y(i),1]; b = [0 0 0]; c = [X(i);Y(i)]; d = -c*a; A((i-1)*2+1:(i-1)*2+2,1:9) = [[a b;b a] d]; %拼接矩阵A,自己对照截图,一次两行,总共2N行end[U S V] = svd(A);h = V(:,9);H = reshape(h,3,3)';
3. 基础矩阵F的计算及前提条件
分别取[xn’,yn’,1],[xn’’,yn’’,1]与F的第一个元素,得到展开式

按照下图定义an和f,得到线性方程
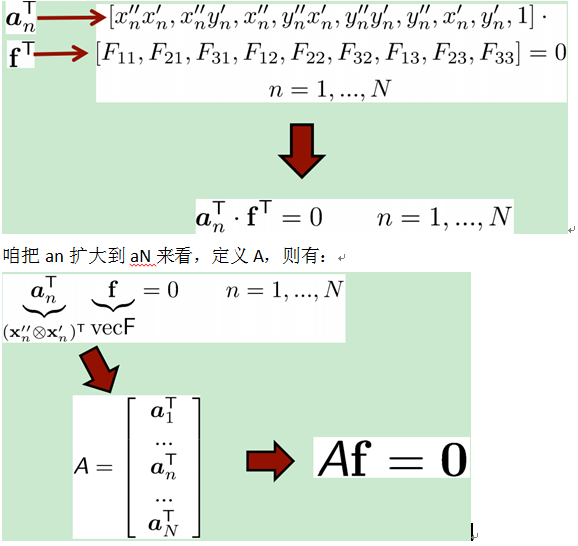
我们同样使用奇异值分解去求Af=0这个方程。由于基础矩阵F是齐次的,矩阵A的秩不大于8,因此我们只要8对匹配点就可以解该方程。实际场景中有可能有不止8对匹配点,而且这些匹配点中存在噪声,矩阵A可能是满秩的(should not be)。此时,我们把A中最小的奇异值对应的奇异向量作为基础矩阵F的解。
通过下图可以清晰得看到SVD全貌,即V的最后一列(对应D的最小的九个奇异值)是F的解。但是这还不够,现在并不能保证F的秩等于2(否则Af全为0了,不符合噪声实际情况)。
现在的目标是使r(F)=2,并且F应该与我们的估计F’无限接近。怎么做?
我们对F本身进行第二次奇异值分解,从F’的奇异值中挑最小的,并将它设置为0.也就是说,根据上一步得到的F’,我们强制修改F’的奇异值,而不改变U’,V’,使得rank(F’)=2。
Matlab代码:
function F = F_from_point_pairs(xs, xss)%xs, xss: Nx3 homologous point coordinates, N>7%F: 3x3 fundamental matrix%coefficient matrixfor n = 1 : size(xs, 1) A(n, :) = kron(xss(n, :), xs(n, :));end%singular value decomposition[U, D, V] = svd(A);%approximate F, possibly regularFa = reshape(V(:,9), 3, 3)';% svd decomposition of F[Ua, Da, Va] = svd(Fa);%algebraically best F, singularF = Ua * diag([Da(1,1), Da(2,2), 0]) * Va';
注:
在求单应性矩阵时扯到过坐标归一化,防止numerically unstable,这里详细讲下。
数值不稳定是指,比如对于一副3000*4000的图片,由于其图片像素坐标过大,使得计算结果不稳定。我们按照下图所示,将原点移动到图像中心,将像素点坐标约束到(-1,1)。
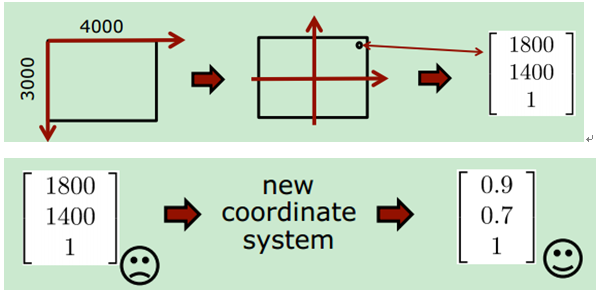
坐标归一化,会改变真实F的值,那么坐标归一化前后基础矩阵的对应关系为:
设存在变换T使得坐标x归一化

哪些情况下,基础矩阵的F会很不稳定?
a.如果所有匹配点对应的物点均在同一平面上,即rank(A)<8,此时Af=0无解。就好比很难对墙面上的画做三维重建
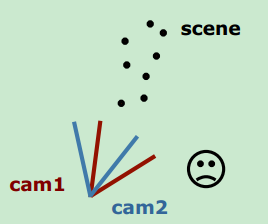
b.如果两个相机的光心重合,即相机没有移动,纯粹旋转,则skew-symmetric矩阵全为0,此时需要考虑使用单应性关系。
4. 本质矩阵E的计算
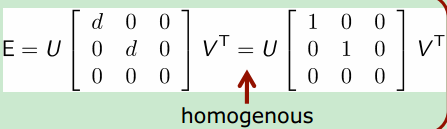
我们可以模仿之前求基础矩阵的方法求本质矩阵,不过此时E的约束关系除了秩必须为2,还要求E的奇异值均为1。
Matlab代码:
function E = E_from_point_pairs(xs, xss)%xs, xss: Nx3 homologous point coordinates, N>7%E: 3x3 fundamental matrix%coefficient matrixfor n = 1 : size(xs, 1) A(n, :) = kron(xss(n, :), xs(n, :));end%singular value decomposition[U, D, V] = svd(A);%approximate F, possibly regularEa = reshape(V(:,9), 3, 3)';% svd decomposition of E[Ua, Da, Va] = svd(Ea);%algebraically best F, singularE = Ua * diag([1, 1, 0]) * Va';
注意:
上面代码函数的输入参数,不是图像坐标,而是乘以相机内参后的图像坐标,xs=K*xs
坐标归一化同样使用此处

5. 给定本质矩阵E,如何计算相对位移关系及相机朝向
给定本质矩阵,我们可以提取R和基线b方向T,但是解并不唯一,实际上有四种!!
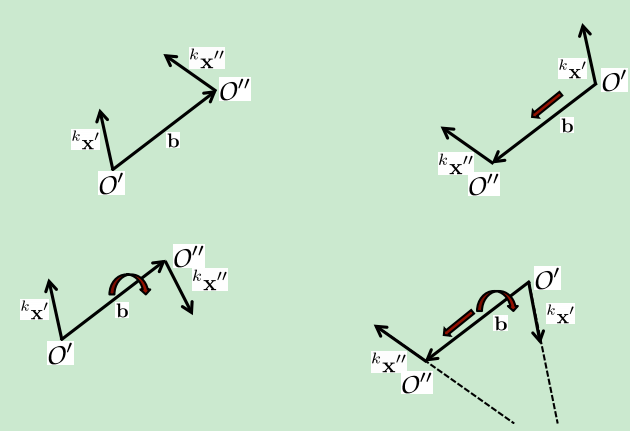
只有左上角这种情况是我们需要的(右上角是绕b旋转了180度,不对的哈),衡量正确与否的标准是:根据R和T复原的点,必须同时位于两个相机的前方。接下来具体展开如何求R和T。
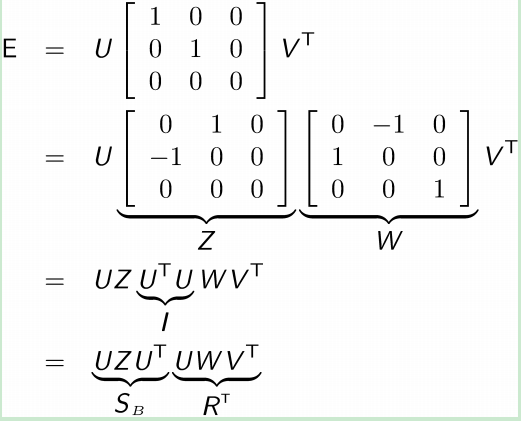
根据E的奇异值分解:

上述做法是从E的两种定义上套用的,现在很轻松的写出基线方向T和旋转矩阵R的表达式。然后这还没完,因为Z和W有尼玛4种组合:
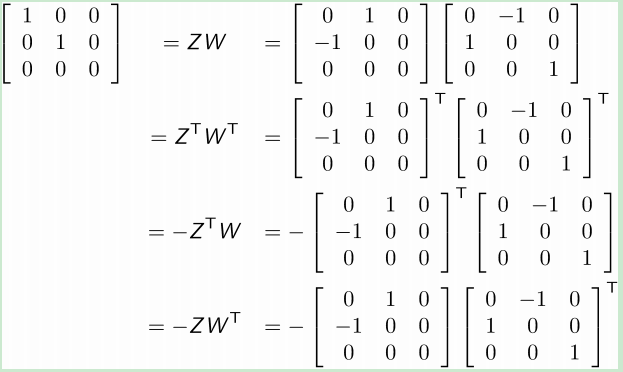
因此E有四种结果,而基线方向T和旋转矩阵R分别有两种情况:
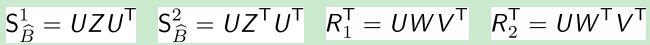
我们测试所有基线方向T和旋转矩阵R组合,还原场景3D坐标(并不是真实尺度),判断所有点是否都位于两个相机的前方,确定唯一的T和R